Datos Generales - Pandeo.

Apartado disponible en el programa base, no necesita ningún módulo adicional.

Este cuadro de diálogo se encuentra dentro de Datos -> Generales, en el grupo General.

Permite seleccionar el método de cálculo empleado para determinar los coeficientes de pandeo (β) de las barras, que determinan la longitud de pandeo de las mismas:

Método de Julian - Lawrence.

El método de Julian - Lawrence calcula la longitud de pandeo de una barra a partir de los valores de rigidez de las vigas y pilares contenidos en el plano de pandeo que nacen de los nudos de la barra

Este método está desarrollado con pequeñas variaciones en diversas normativas:

• Instrucción EHE: en este documento, se utiliza el método de Julian - Lawrence con la formulación de Jackson - Moreland. ESwin utiliza estas fórmulas para el cálculo de longitudes de pandeo.
• Código Técnico de la Edificación y Eurocódigo 3: estas normas emplean el método con la formulación de Wood.

Ambas formulaciones (Jackson - Moreland y Wood) utilizan el mismo planteamiento: el coeficiente β de pandeo es función de los coeficientes de reparto η₁ y η₂ en los nudos extremos de la barra. El coeficiente η viene dado por:

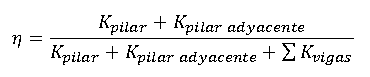
Según estos coeficientes, y sabiendo si se permite el movimiento relativo de los nudos del pilar (estructuras traslacionales) o no (estructuras intraslacionales), el coeficiente β se obtiene directamente de las siguientes expresiones:

	Intraslacional	Traslacional
Jackson - Moreland
Wood

Los resultados de ambos métodos son muy similares, obteniendo valores entre 0,5 y 1 para estructuras intraslacionales y entre 1 y 5 (a partir de 5 tiende a infinito) para estructuras traslacionales, como puede comprobarse en las siguientes gráficas:

 

Cuando se calcula un coeficiente de pandeo en barras de estructuras traslacionales por este método, hay que tener en cuenta que la fórmula de Julian-Lawrence para valores de los dos coeficientes η por encima de 0,9 no es estable, tendiendo a infinito rápidamente. Esto puede tener como consecuencia que resulten esbelteces de las barras con valores excesivos.

Por ejemplo, en la figura siguiente, en el plano del pórtico los coeficientes de reparto en los nudos serán iguales a 0,5 (al ser iguales las tres barras), por lo que el coeficiente de pandeo, considerando la estructura como traslacional, será igual a 1,48.

Ahora bien, en el plano perpendicular al pórtico, el programa no detecta ninguna barra unida a la viga, con lo que aplicando estrictamente el método, los coeficientes de reparto serán iguales a 1 en ambos nudos, con lo que el coeficiente β en teoría vale infinito (el programa tomará un valor finito), resultando una longitud de pandeo disparatada:

Cuando una barra tiene los dos coeficientes de reparto próximos o iguales a 1,00, es porque no existen coacciones a la flexión en sus extremos. En este caso, aun siendo la estructura traslacional, el comportamiento de la barra es asimilable a una viga biarticulada, ya que, aunque se desplacen los nudos, éstos no son capaces de transmitir a la barra una carga que no vaya en su dirección longitudinal. Luego, en estos casos debe forzarse el coeficiente de pandeo a 1,00.

En el caso de pilares, por defecto se calculará el pandeo en ambas direcciones, aunque el usuario podrá omitir cualquier dirección asignando un arriostramiento.

En cualquier caso, cuando se trabaje con estructuras traslacionales, el usuario debe prestar atención a que el coeficiente β no debe ser mayor que 5.

Método de las asimetrías.

Este método se muestra más preciso que el anterior en el caso de pórticos traslacionales con uniones articuladas a la cimentación.

El método de las asimetrías parte de la formulación propuesta en el método anterior para calcular las cargas críticas de pandeo (fórmula de Euler) de todos los pilares del modelo:

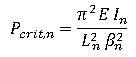
 Una vez obtenida la carga crítica, determina el factor de carga LF, en todas las columnas:

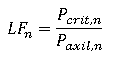
El mínimo de todos los factores LF se denomina coeficiente crítico de pandeo (CCp). Sustituyendo P_crit,n por P_axil,n · CCp, en la ecuación de Euler, se puede obtener un factor β corregido en cada pilar que tiene en cuenta la carga aplicada. Este método es más completo que el de Julian - Lawrence, ya que tiene en cuenta la distribución de cargas sobre los pilares para calcular la longitud de pandeo.

Tipo de edificio

Esta opción determina la fórmula a emplear en el cálculo de los coeficientes b, tanto para el método de Julian-Lawrence como para el método de las asimetrías (basado en el primero).

Tradicionalmente el concepto de traslacionalidad de una estructura ha estado ligado al número de grados de libertad no coartados de los nudos, considerándose traslacionales aquellas estructuras susceptibles de sufrir algún desplazamiento horizontal. Sin embargo, las normas más recientes aplicables al cálculo de estructuras abren un poco más el campo de las estructuras intraslacionales, introduciendo la posibilidad de considerar intraslacional una estructura suficientemente rígida como para que, aunque sufra unos ciertos desplazamientos horizontales, serán despreciables en el cálculo. La Instrucción EHE establece las siguientes definiciones (43.1.1):

• ESTRUCTURAS INTRASLACIONALES: aquellas cuyos nudos, bajo solicitaciones de cálculo, presentan desplazamientos transversales cuyos efectos pueden ser despreciados desde el punto de vista de la estabilidad del conjunto.

• ESTRUCTURAS TRASLACIONALES: aquellas cuyos nudos, bajo solicitaciones de cálculo, presentan desplazamientos transversales cuyos efectos no pueden ser despreciados desde el punto de vista de la estabilidad del conjunto.

En la misma línea, el CTE-DB-SE define este concepto de forma más abierta, permitiendo incluso cuantificar la traslacionalidad por medio del cálculo de un cierto coeficiente.