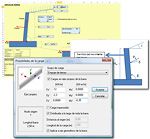
Desde la versión 1.8.1.8, ESwin permite definir la estratigrafía del terreno del trasdós para los muros de hormigón, determinando automáticamente las cargas trapezoidales que solicitan al muro en su trasdós y las cargas producidas por el terreno sobre las zapatas.
 |
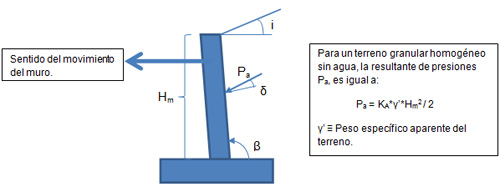
Se define el empuje de tierras como la acción que ejerce el terreno situado en el trasdós de un muro, sobre este y su cimentación. Existen tres tipos de empujes:
|
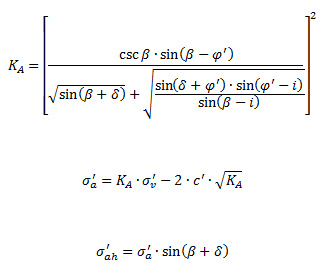
Donde:
KA ≡ Coeficiente de empuje activo.
β ≡ Ángulo en radianes que forma el plano del trasdós con la horizontal (medido en sentido contrario a las agujas del reloj).
φ’ ≡ Ángulo de rozamiento interno efectivo del terreno del trasdós (radianes).
δ ≡ Ángulo de rozamiento entre el terreno del trasdós y el muro (radianes).
i ≡ Ángulo en radianes que forma el plano de la superficie del terreno del trasdós con la horizontal (medido en sentido contrario a las agujas del reloj). Notar que por estabilidad este ángulo no puede ser superior al ángulo de rozamiento interno φ’.
c’ ≡ Cohesión efectiva del terreno (kN/m2). Notar que este parámetro es muy variable con las condiciones de humedad y salvo estudio geotécnico que lo avale para terreno de trasdós, este valor debe ser cero, ya que afecta mucho a la seguridad del muro por reducir en gran medida el empuje.
σv’ ≡ Presión efectiva vertical (kN/m2). En el caso de un terreno del trasdós homogéneo y sin nivel freático, es igual al producto del peso específico aparente del terreno por la profundidad.
σa’ ≡ Presión principal efectiva sobre el plano del trasdós (kN/m2). El ángulo que forma dicha presión con la perpendicular al trasdós del muro es igual a δ, (ángulo de rozamiento muro-terreno).
σah’ ≡ Presión efectiva horizontal sobre el plano del trasdós (kN/m2).
Reposo: Es el empuje que se da normalmente en los muros que tienen anclajes o tienen coartado su movimiento en coronación (muros de sótano). La rigidez de estos muros es grande y no permiten que se produzca la deformación necesaria para movilizar el empuje activo. Para el cálculo de dicho empuje se obtiene el coeficiente de empuje en reposo, que relaciona la presión vertical del terreno con la presión horizontal sobre una superficie dada.
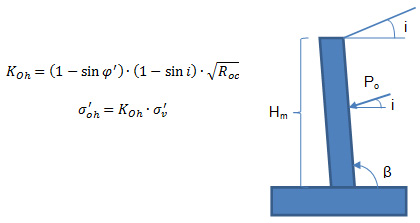
Donde:
KOh ≡ Coeficiente de empuje en reposo horizontal.
φ’ ≡ Ángulo de rozamiento interno efectivo del terreno del trasdós (radianes).
Roc ≡ Razón de sobreconsolidación, que es igual a la relación entre la presión efectiva máxima que ha soportado el suelo a lo largo de su historia geológica y la presión efectiva actual. No es válido el modelo para valores muy altos, superiores a 25-30.
i ≡ Ángulo en radianes que forma el plano de la superficie del terreno del trasdós con la horizontal (medido en sentido contrario a las agujas del reloj). Notar que por estabilidad este ángulo no puede ser superior al ángulo de rozamiento interno φ’.
σv’ ≡ Presión efectiva vertical (kN/m2). En el caso de un terreno del trasdós homogéneo y sin nivel freático, es igual al producto del peso específico aparente del terreno por la profundidad.
σoh’ ≡ Presión efectiva horizontal sobre el plano del trasdós (kN/m2). El ángulo que forma la presión de empuje en reposo con la horizontal es igual a i, (ángulo de inclinación del terreno del trasdós).
Pasivo: Es el empuje que se produce como resistencia que opone el terreno del intradós al desplazamiento del muro contra él. Este empuje se moviliza con grandes desplazamientos del orden de la centésima parte de la altura, lo que añadido a la exigencia de que el terreno del intradós no varíe a lo largo de toda la vida de la estructura, hace que en la gran mayoría de los casos sea incompatible con las condiciones de funcionalidad y seguridad. Para el cálculo de dicho empuje se obtiene el coeficiente de empuje pasivo, que relaciona la presión vertical del terreno con la presión principal sobre una superficie dada
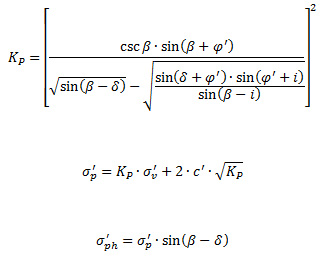
Donde:
KP ≡ Coeficiente de empuje pasivo.
β ≡ Ángulo en radianes que forma el plano del trasdós con la horizontal (medido en sentido contrario a las agujas del reloj).
φ’ ≡ Ángulo de rozamiento interno efectivo del terreno del trasdós (radianes).
δ ≡ Ángulo de rozamiento entre el terreno del trasdós y el muro (radianes).
i ≡ Ángulo en radianes que forma el plano de la superficie del terreno del trasdós con la horizontal (medido en sentido contrario a las agujas del reloj). Notar que por estabilidad este ángulo no puede ser superior al ángulo de rozamiento interno φ’.
c’ ≡ Cohesión efectiva del terreno (kN/m2). Notar que este parámetro es muy variable con las condiciones de humedad y salvo estudio geotécnico que lo avale para terreno de trasdós, este valor debe ser cero, ya que afecta mucho a la seguridad del muro por aumentar en gran medida el empuje pasivo.
σv’ ≡ Presión efectiva vertical (kN/m2). En el caso de un terreno del trasdós homogéneo y sin nivel freático, es igual al producto del peso específico aparente del terreno por la profundidad.
σp’ ≡ Presión principal efectiva sobre el plano del trasdós (kN/m2). El ángulo que forma dicha presión con la perpendicular al trasdós del muro es igual a δ, (ángulo de rozamiento muro-terreno).
σph’ ≡ Presión efectiva horizontal sobre el plano del trasdós (kN/m2).
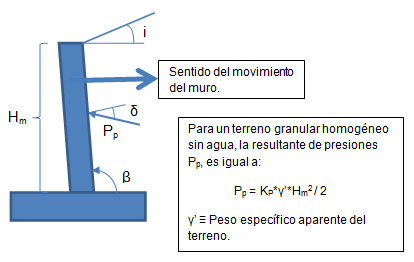
Dado que el empuje pasivo es una fuerza estabilizante cuya consideración influye notablemente sobre el valor de los coeficientes de seguridad del muro; y dado que su movilización está condicionada por un desplazamiento excesivo del muro y por la no variación a lo largo de la vida de éste, de las condiciones del terreno del intradós (tanto en cota, como en características), las normativas suelen ser muy restrictivas en su utilización para cimentaciones superficiales.
Debido a esto en el cálculo de la estabilidad de un muro normal se desprecia el empuje pasivo y se considera como acción desestabilizante el empuje activo para muros ménsula no impedidos en su movimiento de flexión, y el empuje al reposo para muros de sótano o anclados (los cuales tienen restricciones en su movimiento de flexión). También se debe de considerar el empuje al reposo en aquellos muros en los que se quiera ser muy restrictivo en su movimiento, debido a su afección a instalaciones o estructuras anexas muy sensibles al movimiento del muro.
En el caso de existencia de agua en el trasdós del muro, hay que sumar al valor de la presión en un punto obtenida con las fórmulas anteriores, (considerando el peso específico sumergido del terreno en lugar del peso específico aparente), la presión intersticial del agua en ese punto.
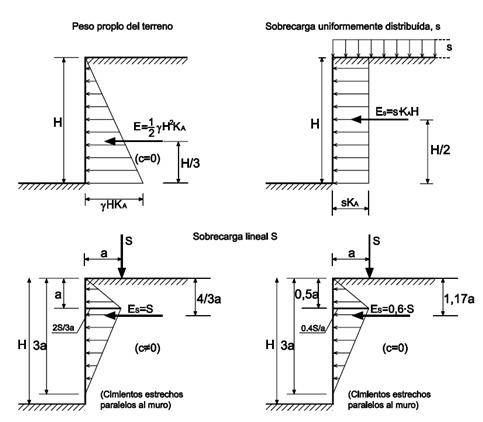
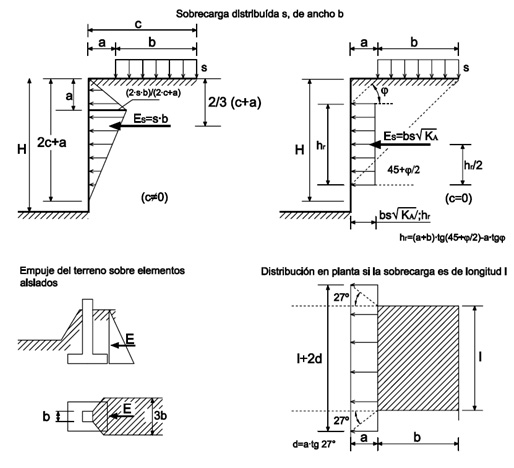
Si queremos considerar en el muro la acción de las sobrecargas sobre el terreno del trasdós, se hará aplicando el criterio simplificado recogido por la CTE-DB-SE-C, siempre que estas sobrecargas sean moderadas.
Dado que el empuje pasivo es una fuerza estabilizante cuya consideración influye notablemente sobre el valor de los coeficientes de seguridad del muro; y dado que su movilización está condicionada por un desplazamiento excesivo del muro y por la no variación a lo largo de la vida de éste, de las condiciones del terreno del intradós (tanto en cota, como en características), las normativas suelen ser muy restrictivas en su utilización para cimentaciones superficiales.
Debido a esto en el cálculo de la estabilidad de un muro normal se desprecia el empuje pasivo y se considera como acción desestabilizante el empuje activo para muros ménsula no impedidos en su movimiento de flexión, y el empuje al reposo para muros de sótano o anclados (los cuales tienen restricciones en su movimiento de flexión). También se debe de considerar el empuje al reposo en aquellos muros en los que se quiera ser muy restrictivo en su movimiento, debido a su afección a instalaciones o estructuras anexas muy sensibles al movimiento del muro.
En el caso de existencia de agua en el trasdós del muro, hay que sumar al valor de la presión en un punto obtenida con las fórmulas anteriores, (considerando el peso específico sumergido del terreno en lugar del peso específico aparente), la presión intersticial del agua en ese punto.
Si queremos considerar en el muro la acción de las sobrecargas sobre el terreno del trasdós, se hará aplicando el criterio simplificado recogido por la CTE-DB-SE-C, siempre que estas sobrecargas sean moderadas.
Aplicación ESwin - Estructuras Tridimensionales
Una de las virtudes del programa de estructuras tridimensionales ESwin es la libertad que tiene el usuario a la hora de definir la geometría de la estructura y por tanto de los muros y su cimentación.

Debido a esto la aplicación de las cargas automáticamente sobre el muro se complica por la gran multiplicidad de casos que se pueden dar. Actualmente se está trabajando en ello y se espera que a lo largo de este año se pueda publicar una actualización con la aplicación automática de las cargas de empuje de tierra sobre los elementos de la estructura y la cimentación.
En el caso que el usuario quiera calcular con el ESwin un muro sometido a empuje de tierras deberá introducir las presiones inicial y final de la ley trapezoidal en el cuadro de propiedades del muro en la pestaña de “Cargas Trapezoidales”.
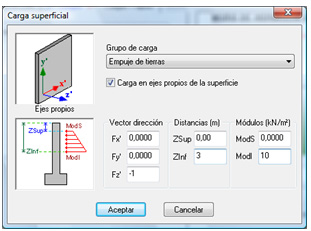
Donde:
- Grupo de carga: Indica el grupo al que pertenecerá la carga definida; normalmente se escoge “Empuje de tierras”.
- Carga en ejes propios de la superficie: con esta opción activada, las cargas se podrán referir a los ejes locales (x´, y´, z´) del muro y no a los ejes globales de la estructura.
- Vector de dirección (Fx’, Fy’, Fz’): Indica la dirección de la carga, a través de las tres componentes del vector de dirección. En los casos más habituales, si define las cargas en ejes locales, el vector de dirección se indica como sigue:
- Si la carga es perpendicular al muro y despreciamos su componente vertical, sería:
Hacia el interior: 0, 0, -1.
Hacia el exterior: 0, 0, 1. - Distancias: Las distancias indican qué porción de muro es abarcada por la carga superficial. La distancia Zsup es la que hay entre el borde superior de la carga y el borde superior del muro. La distancia ZInf es la distancia que hay entre el borde inferior de la carga y el borde superior del muro.
- Módulos: Es el valor de la carga, en kN/m2, en el borde superior (ModS) y en el borde inferior (ModI).
Además deberá introducir el peso de las tierras sobre el talón de la zapata corrida y el empuje de las tierras sobre el canto de la zapata.
El peso de las tierras se introduce a través del cuadro de propiedades de la zapata corrida en la pestaña de “Tierras”.
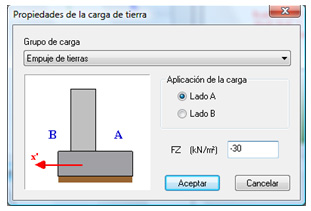
- Grupo de carga: Indica el grupo al que pertenecerá la carga definida, el mismo que la carga sobre el muro; normalmente se escoge “Empuje de tierras”.
- Aplicación de la carga: Sirve para seleccionar la zona donde se encuentra la carga de tierra respecto al eje local de la zapata corrida.
- FZ: Valor de la presión de tierra en kN/m2 respecto al eje global Z, producida por el peso de las tierras que gravitan sobre el talón de la zapata. El valor por tanto debe ser negativo para representar el peso de las tierras.
El empuje de las tierras sobre el canto de la zapata corrida se introduce a través del cuadro de propiedades de la zapata corrida en la pestaña de “Cargas”.
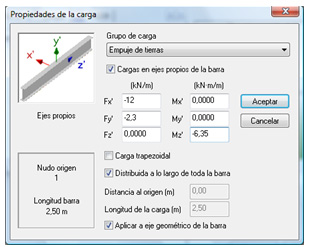
- Grupo de carga: Indica el grupo al que pertenecerá la carga definida, el mismo que la carga sobre el muro; normalmente se escoge “Empuje de tierras”.
- Fx’, Fy’, Fz’: Resultante de presiones del empuje de las tierras sobre el canto de las zapatas en kN/m. Notar que estos valores son dependientes del canto de la zapata, y por tanto debe recalcularlos el usuario si modifica dicho canto. La componente principal será Fx’ y en el caso que se quiera considerar la componente vertical del empuje se introducirá Fy’ con valor negativo.
- Mx’, My’, Mz’: Resultante de momento producido por las presiones del empuje de las tierras sobre el canto de las zapatas en kN*m/m. Notar que estos valores son dependientes del canto de la zapata, y por tanto deben ser recalculados si se modifica dicho canto. El empuje de tierras únicamente produce la componente Mz’.
- Carga trapezoidal: Se marca esta opción si la carga es de tipo trapezoidal y por tanto varía a lo largo de la longitud de la barra.
- Distribuida a lo largo de toda la barra: Se marca esta opción si la carga es distribuida y ocupa toda la zapata corrida.
- Aplicar a eje geométrico de la barra: Se marca esta opción si la carga está referida al eje geométrico de la zapata corrida, es decir, al eje directriz afectado por la excentricidad introducida en la pestaña de “Crecimiento”. Si no se marca la carga se aplica directamente a la directriz de la zapata corrida.
Dado que el calcular todos estos valores puede ser algo engorroso para el usuario se ha diseñado una hoja de cálculo, en la que introduciendo los datos básicos de terreno y sobrecarga uniforme aplicada en el trasdós, se obtienen los valores ha introducir en estos cuadros de diálogo.
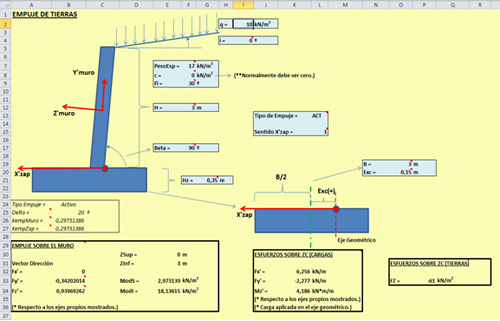
Puede descargarla en el siguiente enlace:
|
Empuje de tierras sobre muros y zapatas corridas. Aplicación a ESwin. (299KB) |
|
| Hoja excel cálculo de empuje (138KB) |
